7 Uncertainty analysis
Uncertainty analysis, akin to sensitivity analysis, is primarily concerned with assessing the uncertainty in the outcomes of a model. The ideal approach involves conducting both uncertainty and sensitivity analyses concurrently, usually initiating with the uncertainty analysis (Saltelli et al. 2008). For this purpose, the data acquired from the sensitivity analysis will be utilized to carry out the uncertainty analysis as well.
Running the process rate estimator repeatedly on sets of parameters drawn from their respective distributions of uncertainty yielded a data frame of estimated process rates. In the last chapter, we analyzed the relationship between the parameters and the estimated process rates. In this context, we called the matrix with the estimated process rates \(\mathbf Y\), where \(\mathbf Y \in \mathbb R^{n \times 3}\) with \(n\) samples drawn in total. With the uncertainty analysis, we’ll specifically investigate the process rates without considering the parameters. Thus, the process rates will be called \(\mathbf X\) in this context.
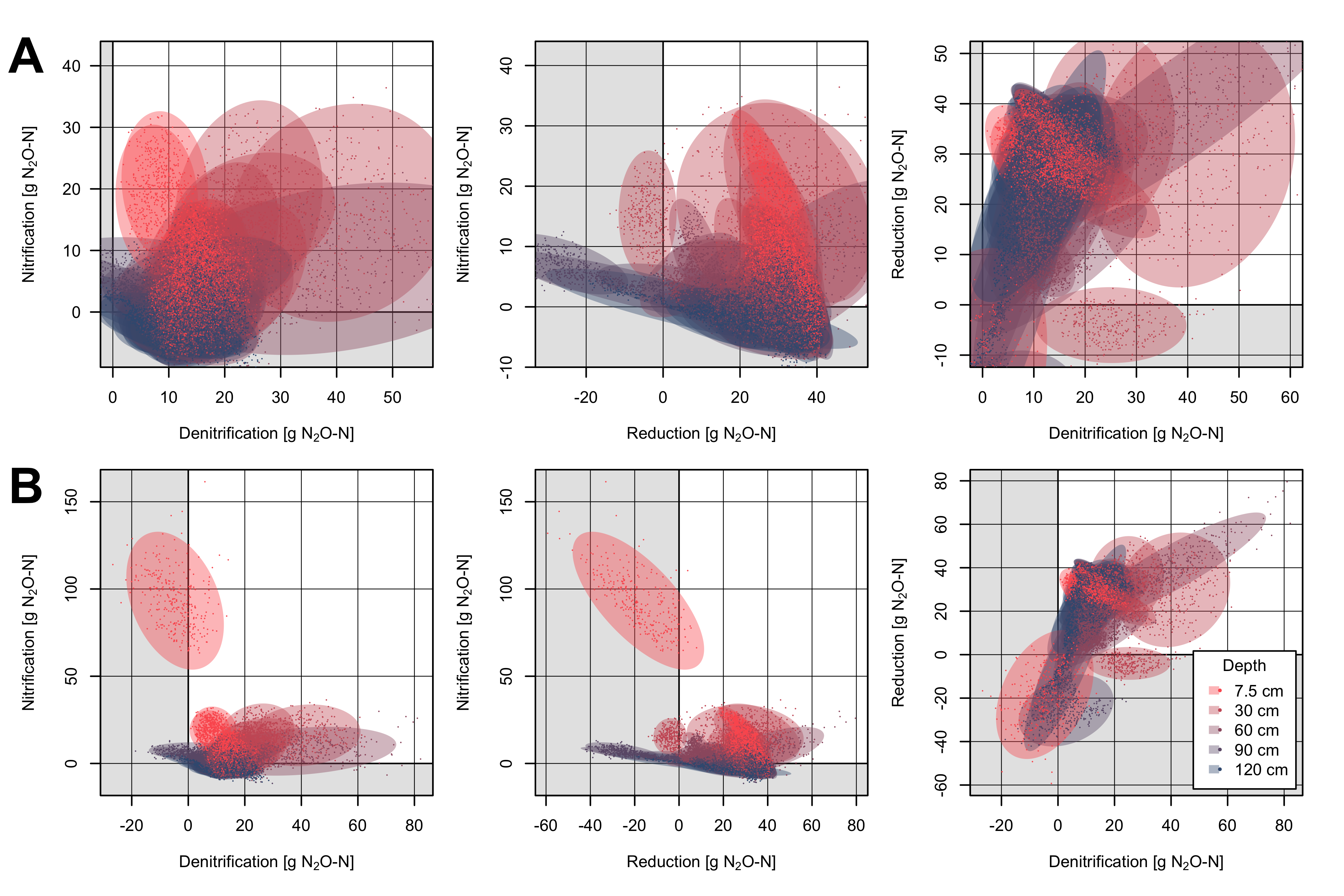
Two things are striking when looking at the clusters in figure 7.1: Both the within-group variance as well as the total variance (i.e. the variance of the cluster location) seems to be lower for the deeper depths. Additionally, one of the cluster centers constitutes a massive outlier – it’s column 12 at 7.5 cm depth (Figure 7.1 B).
7.1 Quantifying uncertainty
To quantify the uncertainty surrounding each parameter in the processes depicted, a method to summarize the set of estimated processes is needed. Since all distributions seem to be multivariate Gaussians, covariance matrices \(\mathbf\Sigma\) are well fit to describe them. Utilizing a matrix norm presents a viable approach to further reduce each covariance matrix \(\mathbf\Sigma\) to one number. For this, we’ll use the determinant \(\det(\mathbf\Sigma)\), which provides a measure of the total variance contained within the multivariate Gaussian distribution.1
1 Alternatives to reduce the covariance matrix \(\mathbf\Sigma\) to a scalar would be the trace of the covariance matrix \(\text{tr}(\mathbf\Sigma)\) or the Frobenius norm.
Although the trace gives us a measure of the total variance, it does not take into account the correlation between variables.
Similarly, the Frobenius norm is less effective than the determinant in measuring the “volume” of a \(\mathbf\Sigma\) because it sums the squares of all matrix elements without capturing the multidimensional shape and scale interactions that the determinant reflects.
\[\det{\mathbf \Sigma} = \det (\operatorname {cov} \mathbf X) = \det \left[{\frac {1}{n}}\left(\mathbf {X} \mathbf {X} ^{\top }-{\frac {1}{n}}\mathbf {X} \mathbf I \mathbf {X} ^{\top }\right) \right] \tag{7.1}\]
The determinants of each clusters covariance matrix \(\mathbf \Sigma\) in figure 7.1 are represented in figure 7.2. Not surprisingly, it is by orders of magnitude larger for column 12 at 7.5 cm depth than for the other clusters.
7.2 Process rate estimates with respective uncertainties
In the end, the values from our uncertainty analysis are the best guess of the actual uncertainty of each estimate. Table 7.1 showcased the mean estimates with their respective standard deviation computed from the uncertainty analysis.
| 7.5 cm | 30 cm | 60 cm | 90 cm | 120 cm | |
|---|---|---|---|---|---|
| 1 | 8.4±4.1 | 1.9±4.3 | 0.58±2.7 | -0.57±3 | -0.71±2.7 |
| 2 | 4.8±4.2 | 12±5.2 | 3.2±3.2 | 0.031±2.5 | -0.86±2.5 |
| 3 | 4.7±4.5 | 5.7±4.7 | 2.7±4 | 1.5±3.3 | 0.44±3.1 |
| 4 | 5.9±4.3 | 18±6.9 | 8.7±3.8 | 2.2±2 | -0.064±2.8 |
| 5 | 6.2±4.5 | 6.3±4.3 | 0.46±3.5 | -0.47±3.5 | -1.2±3.3 |
| 6 | 5.4±4.2 | 4.1±4.3 | 1.7±4.1 | 3.2±4.9 | 2.2±4.1 |
| 7 | 4.8±4.5 | 1.9±4.2 | 3.9±3 | 2±3.5 | 1.3±3.3 |
| 8 | 8.9±3.9 | 4.6±4.1 | 1.6±3.6 | 0.29±3.4 | -0.49±3.3 |
| 9 | 20±5 | 16±7.2 | 7±5.7 | 7.1±2.1 | -0.29±2.7 |
| 10 | 4.1±3.7 | 6.5±4.1 | 3.3±2.9 | 0.44±3.1 | 1.5±3.7 |
| 11 | 18±5 | 6±4.9 | -1.6±2.9 | -2.5±2.3 | -2.4±2.1 |
| 12 | 93±16 | 15±4.3 | 5.3±2.9 | 2.8±2.7 | -2.2±2.2 |
| 7.5 cm | 30 cm | 60 cm | 90 cm | 120 cm | |
|---|---|---|---|---|---|
| 1 | 16±3.3 | 15±3.8 | 12±4 | 13±4 | 12±4.3 |
| 2 | 14±3.1 | 20±4.1 | 15±3.8 | 12±4.7 | 12±5 |
| 3 | 14±3.3 | 17±3.1 | 19±5.4 | 15±3.8 | 13±4.1 |
| 4 | 15±3.3 | 24±5.4 | 12±2.6 | 6.6±3.5 | 11±4 |
| 5 | 14±3 | 14±3.2 | 15±4.2 | 15±4 | 16±4.4 |
| 6 | 15±3.1 | 14±3.5 | 15±4 | 14±3.4 | 14±3.6 |
| 7 | 15±3.4 | 19±3.7 | 11±4.2 | 13±3.9 | 12±4.1 |
| 8 | 16±3.2 | 15±3.4 | 16±4.7 | 16±4.5 | 16±4.8 |
| 9 | 9.3±3.2 | 41±8.2 | 40±14 | 2.8±6.9 | 7.2±6.9 |
| 10 | 17±3.5 | 16±3.6 | 13±4.2 | 14±4.4 | 15±4 |
| 11 | 7.9±3 | 22±5.1 | 15±4.6 | 13±5.3 | 9.9±5.6 |
| 12 | -4.7±7 | 25±6 | 16±6.6 | 2.6±6 | 10±5.2 |
| 7.5 cm | 30 cm | 60 cm | 90 cm | 120 cm | |
|---|---|---|---|---|---|
| 1 | 29±3.1 | 35±3.7 | 28±4 | 32±4.1 | 30±4.4 |
| 2 | 35±3.5 | 30±4.6 | 21±6.3 | 24±6.1 | 25±5.1 |
| 3 | 34±3.6 | 31±4.3 | 33±3.6 | 29±3.9 | 29±3.1 |
| 4 | 33±3.4 | 35±7.9 | 8.7±2.9 | 10±11 | 28±6.6 |
| 5 | 33±3.4 | 33±3 | 32±2.7 | 35±2.6 | 35±2.7 |
| 6 | 33±3.2 | 32±3.1 | 35±3.5 | 35±3.7 | 36±3.4 |
| 7 | 34±3.6 | 33±3.6 | 21±8.5 | 29±2.7 | 28±3.4 |
| 8 | 25±2 | 34±3.2 | 30±2.6 | 32±2.9 | 33±2.7 |
| 9 | 28±4 | 30±11 | 40±10 | -26±6.8 | 10±17 |
| 10 | 32±2.9 | 32±3.4 | 22±4.9 | 30±2 | 34±2.7 |
| 11 | 30±3.8 | 23±3.9 | 24±8.4 | 23±7.7 | 19±9.2 |
| 12 | -18±12 | -4±3.1 | 7.1±5.3 | -6.1±16 | 22±8.7 |