3 Data preparation

This chapter describes the data used for the process rate estimator as well as how it is pre-processed and how new variables are calculated.

3.1 Description of the measurements

The study uses data collected from a mesocosm experiment – i.e. an outdoor experiment that examines the natural environment under controlled conditions. The experiment was set up as a randomized complete block design, with 4 varieties and 3 replicates, using 12 non-weighted lysimeters. A non-weighted lysimeter is a device to measure the amount of water that drains through soil, and to determine the types and amounts of dissolved nutrients or contaminants in the water. Each lysimeter had five sampling ports with soil moisture probes and custom-built pore gas sample, at depths of 7.5, 30, 60, 90 and 120 cm below soil surface.

\[4 \times 3 \times 5 \times 161 = 9660 \tag{3.1}\]

Equation 3.1 shows how many observations we should expect to have. In reality, some observations are missing. Hence, the measurements data frame only includes 9558 rows, with 9 variables. Table 3.1 gives an overview of those variables.

Table 3.1: Overview of the variables included in the `measurements` data as included in the R package `PRE`. For the continuous variables, a histogram shows the measurements distribution.

Code	Name	Description	Class	Missing
`date`	Date	Date of a measurement in the `"Date"` format (`YYYY-MM-DD`), ranging from August 27 2015 to February 3 2016.	`"Date"`	0%
`column`	Column	Factor variable indicating one out of twelve experimental units.	`"ordered"`	0%
`depth`	Measurement depth	Depth of the measurement, either 7.5, 30, 60, 90, or 120 cm.	`"numeric"`	0%
`increment`	Depth increment	Height of a soil layer from lower to upper boundary.	`"integer"`	0%
`variety`	Wheat variety	Either `CH Claro`, `Monte Calme 268`, `Probus`, or `Zinal`.	`"factor"`	0%
`moisture`	Soil moisture	The moisture is expressed as volumetric water content in cubic meters of water per cubic meters of soil [\(\frac{m^3}{m^3}\)].	`"numeric"`	0%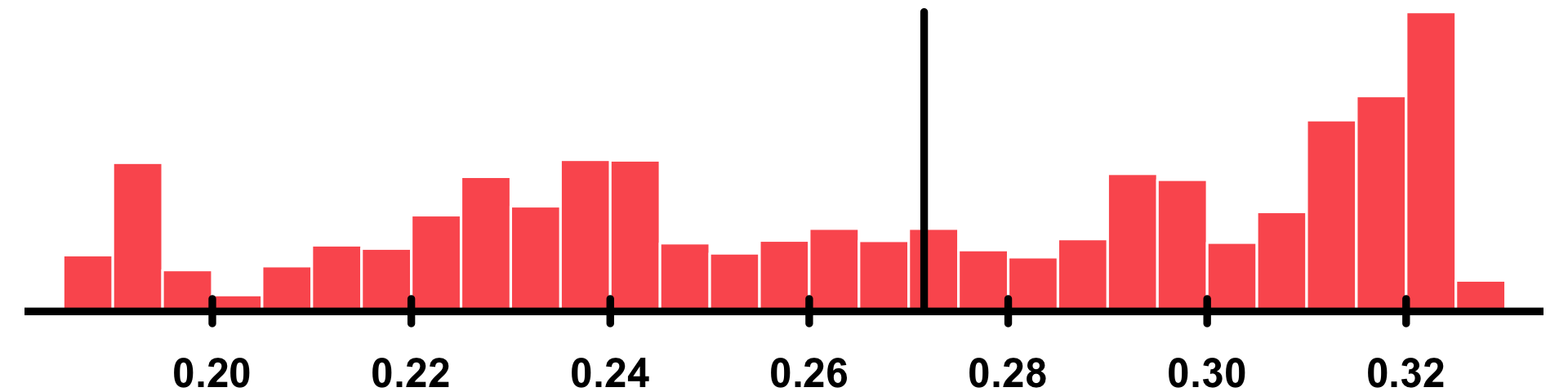
`N2O`	Corrected N₂O concentration		`"numeric"`	86.9%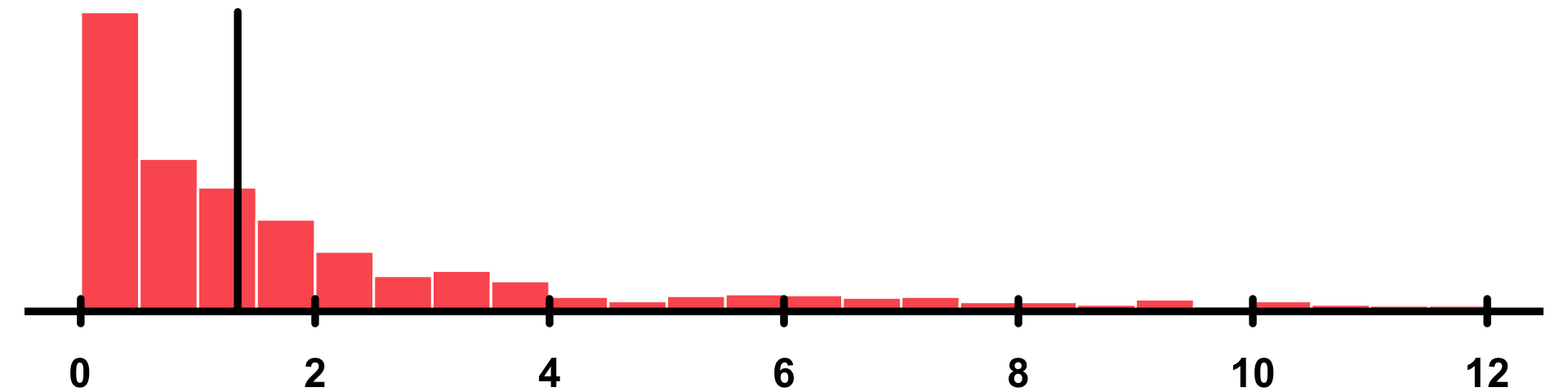
`SP`	Site preference	Site preference values for N₂O	`"numeric"`	86.3%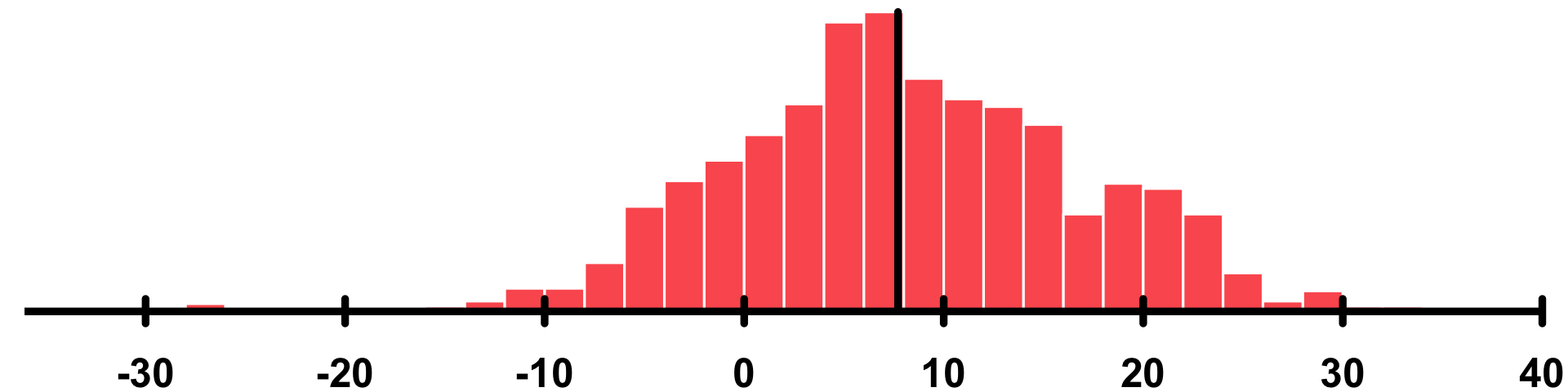
`d18O`	\(\delta^{18}\ce O\) stable isotope ratio	Ratio of stable isotopes oxygen-18 (¹⁸O) and oxygen-16 (¹⁶O).	`"numeric"`	86.3%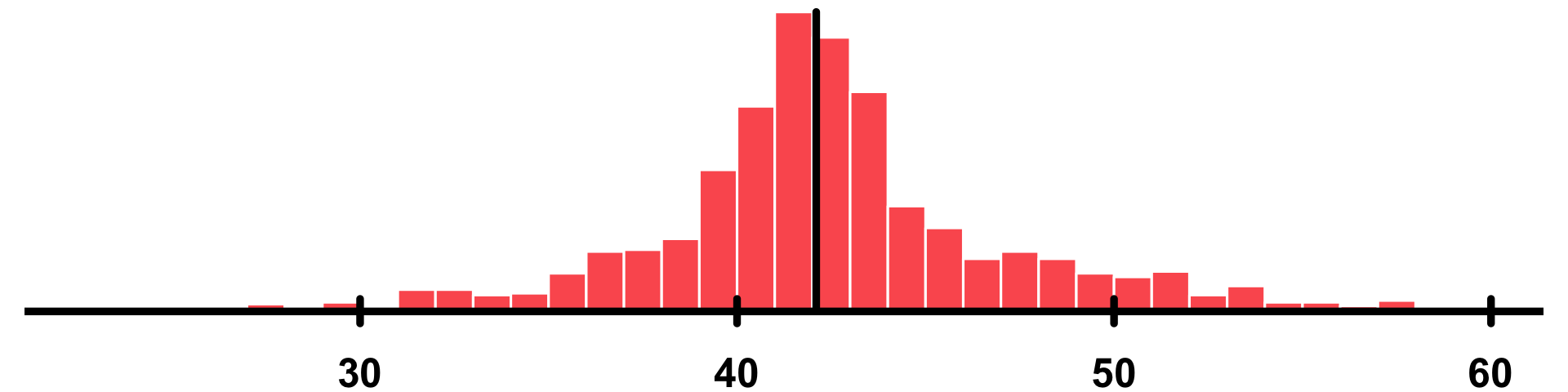

Accessing the measurement data in R

In the R package PRE, this data is available as the object measurements. We can load the data with the data function in R.

data("measurements", package = "PRE")

Upon doing so, a data frame called measurements will appear in our global environment. Alternatively, the data can be directly accessed as PRE::measurements (the prefix PRE:: tells R that the object can be found in the PRE package.)

You can see an interactive overview of the measurements data in the column below. For many dates, there are no measurements of \(\ce{N2O}\), site preference, or \(\delta^{18}\text{O}\).

Luckily, the measurements for N₂O concentration, site preference as well as \(\delta\)¹⁸O are distributed more or less evenly over time. Hence, we’ll interpolate the missing values. This step will be the focus of the next section.

3.2 Calculating volumetric and area N₂O-N

In a first step, we are calculating the N₂O-N per volume and subsequently per area. This is a necessary step, because the process rate estimator requires these variables.

Since both N2ONvolume as well as N2ONarea are dependent on initial parameters, their computation is part of the workflow and might change slightly for a changed experimental set-up or different assumptions regarding the environment.

The volumetric N₂O-N is calculated from the N₂O concentration (Equation 3.2).

\[\text N_2 \text {O-N}_\text{volume} = \frac{28[\text{N}_2\text O]}{\text {R} \cdot \text {T}} \tag{3.2}\]

Here, \(\text {R}\) is the gas constant and \(T\) is the temperature. In a next step, we calculate the per-area N₂O-N from the volumetric N₂O-N and the soil moisture as well as the total porosity and the increment in meters.

\[\text N_2 \text {O-N}_\text{area} = \text N_2 \text {O-N}_\text{volume} \times \frac{1}{100} \texttt{increment} \times \frac{10^4}{10^3} \left(\theta_t - \texttt{moisture} \right) \tag{3.3}\]

All of these equations are implemented in the getN2ON function. This function returns a data frame very similar to measurements, but with two extra columns for the computed N2ONvolume and N2ONarea variables.

data <- getN2ON(data = PRE::measurements, parameters = getParameters())

Note that the getParameters function simply returns a list with the default values for all necessary parameters such as the gas constant \(\text R\) or the assumed air temperature \(\text T\). If we wish to change these, we can pass alternative parameter values to the function. For example, we could assume an air temperature of 300 K with getParameters(temperature = 300). This makes sure that depended parameter values are updated as well.

3.3 Interpolating the measurements

The N₂O concentration, site preference as well as \(\delta\)¹⁸O are estimated as a function of time for every depth and every column, separately. To achieve this function approximation, Kernel Regression as implemented in npreg is used (Hayfield and Racine 2008). The model requires a single parameter, the bandwidth (bws), which defines how flexible it is. However, the bandwidth needs to be actively chosen and cannot be intrinsically estimated – it’s a hypertuning parameter a.k.a. a hyperparameter.

Choosing optimal bandwidths for the interpolation

Figure 3.1 gives an intuitive understanding on why we don’t want to use the same bandwidth for every single combination of depth and column: In some instances we seem to have a very clear signal, while in others, there seems to be much noise – we are dealing with unequal variance, a.k.a. heteroskedasticity.

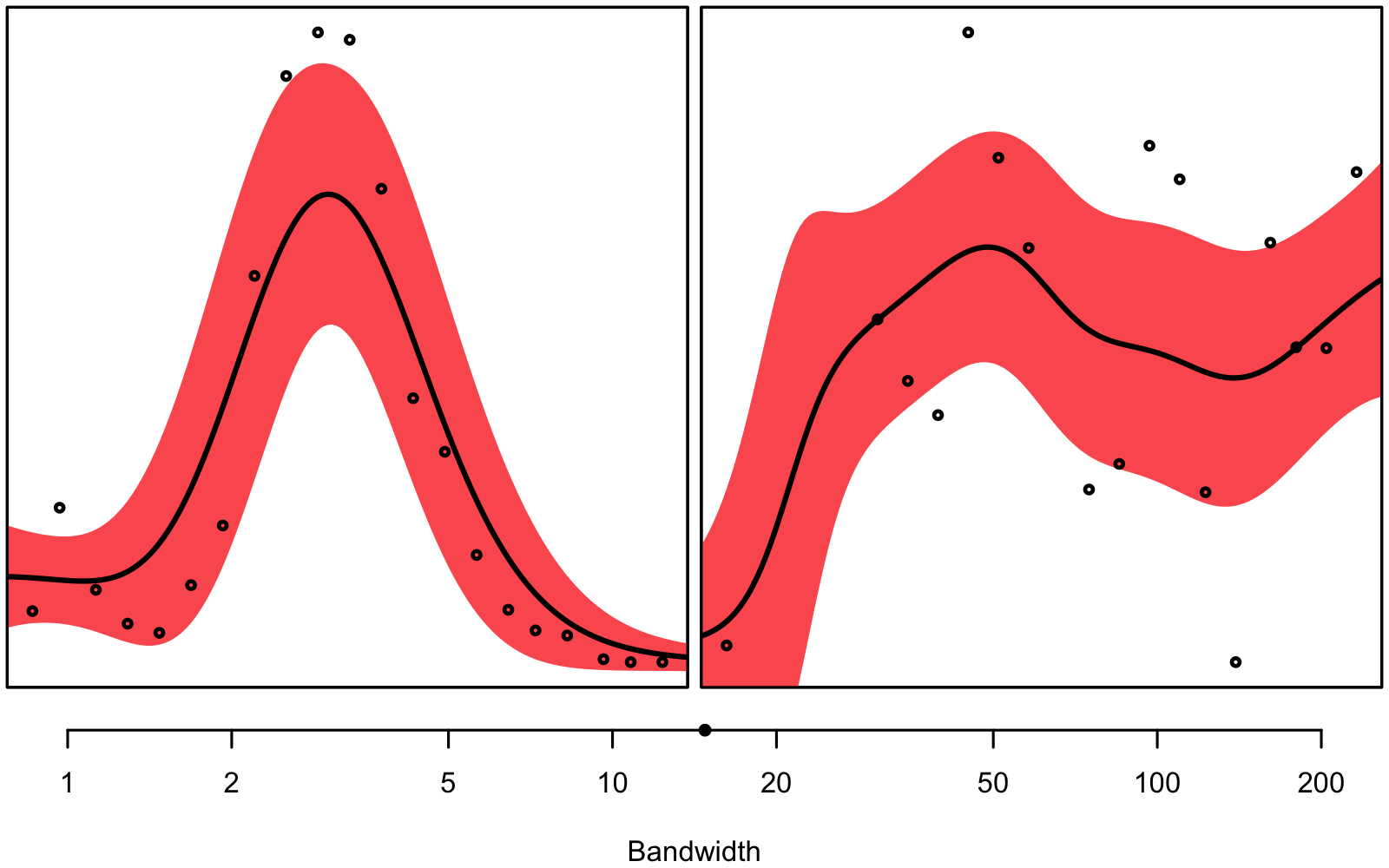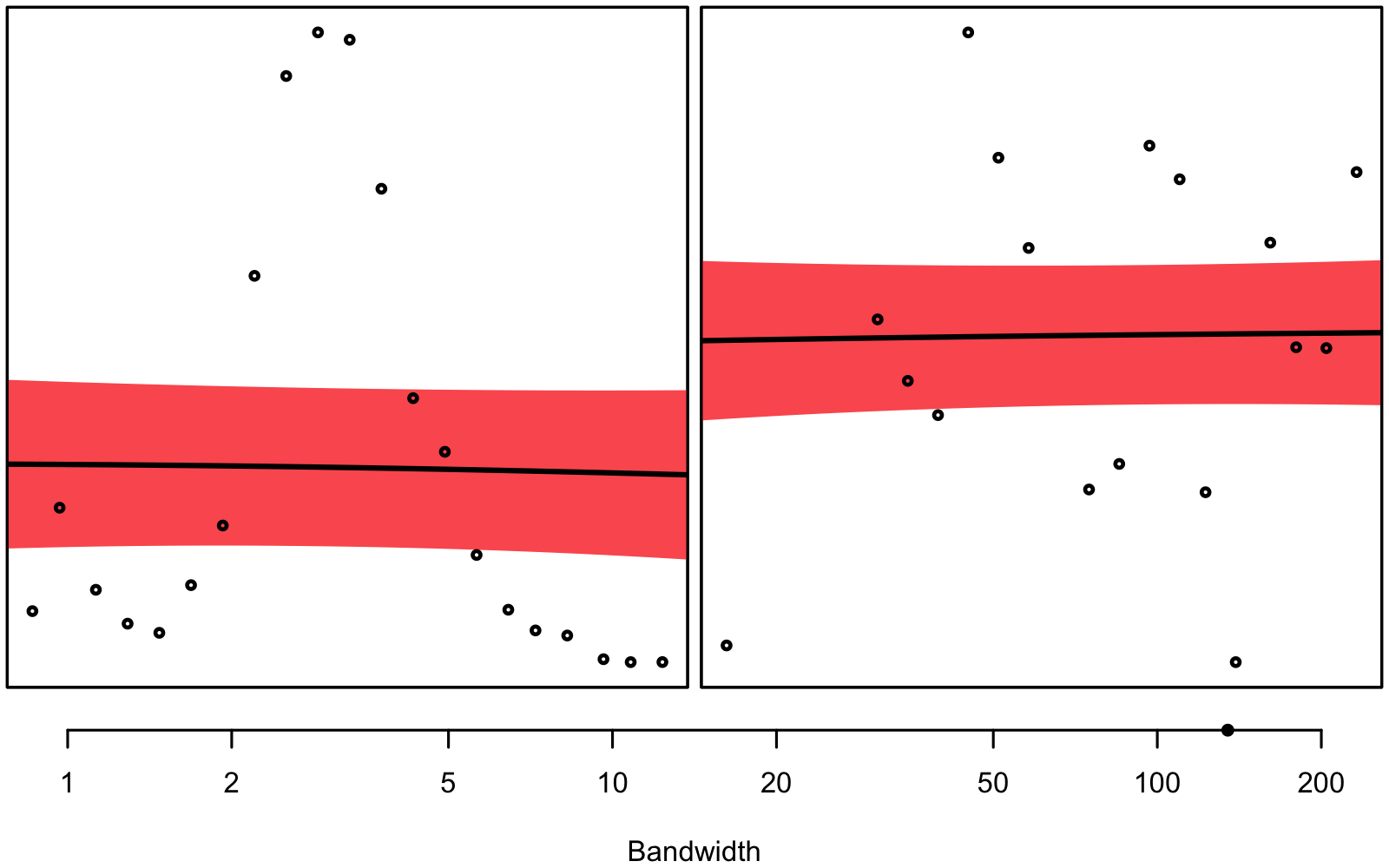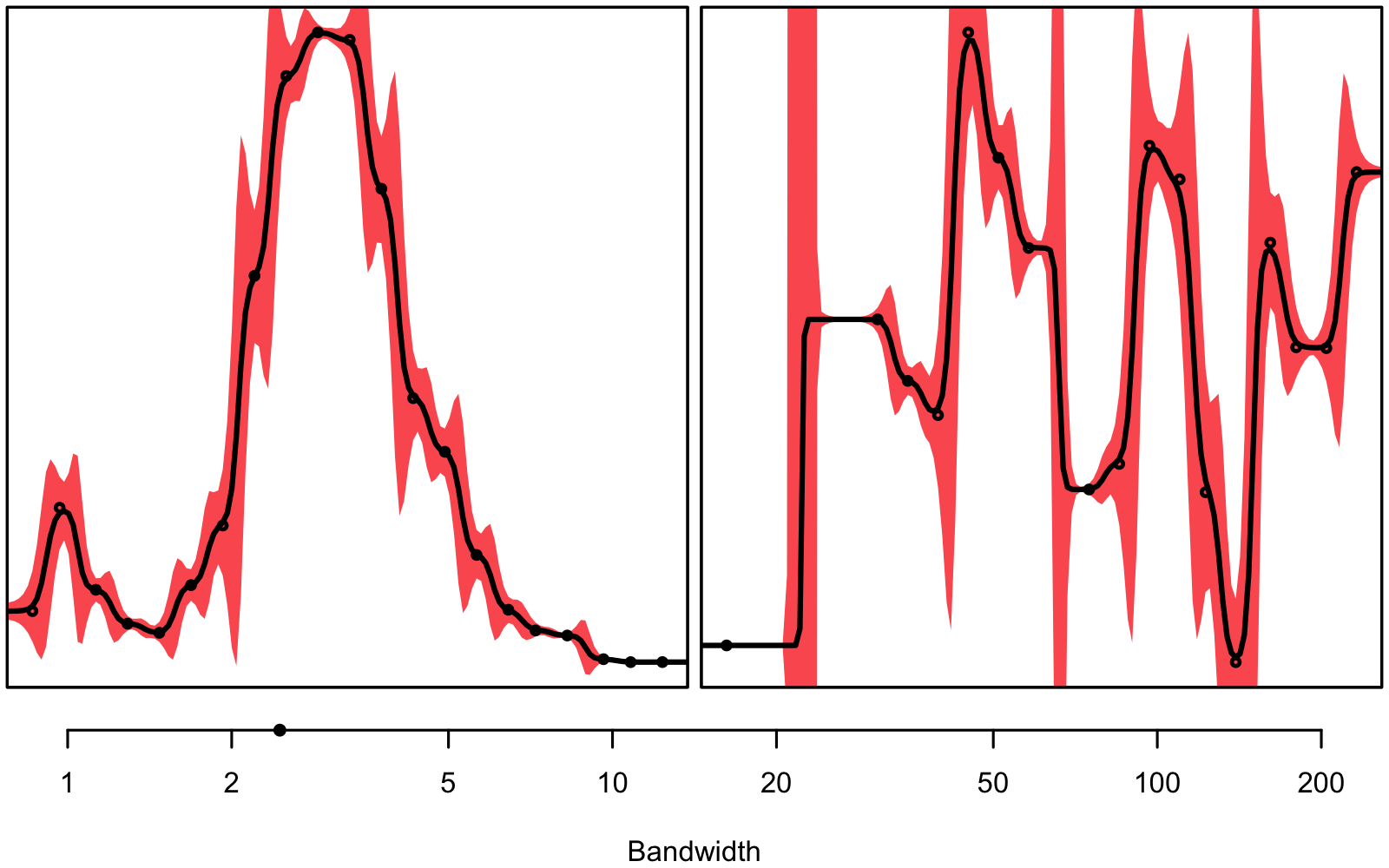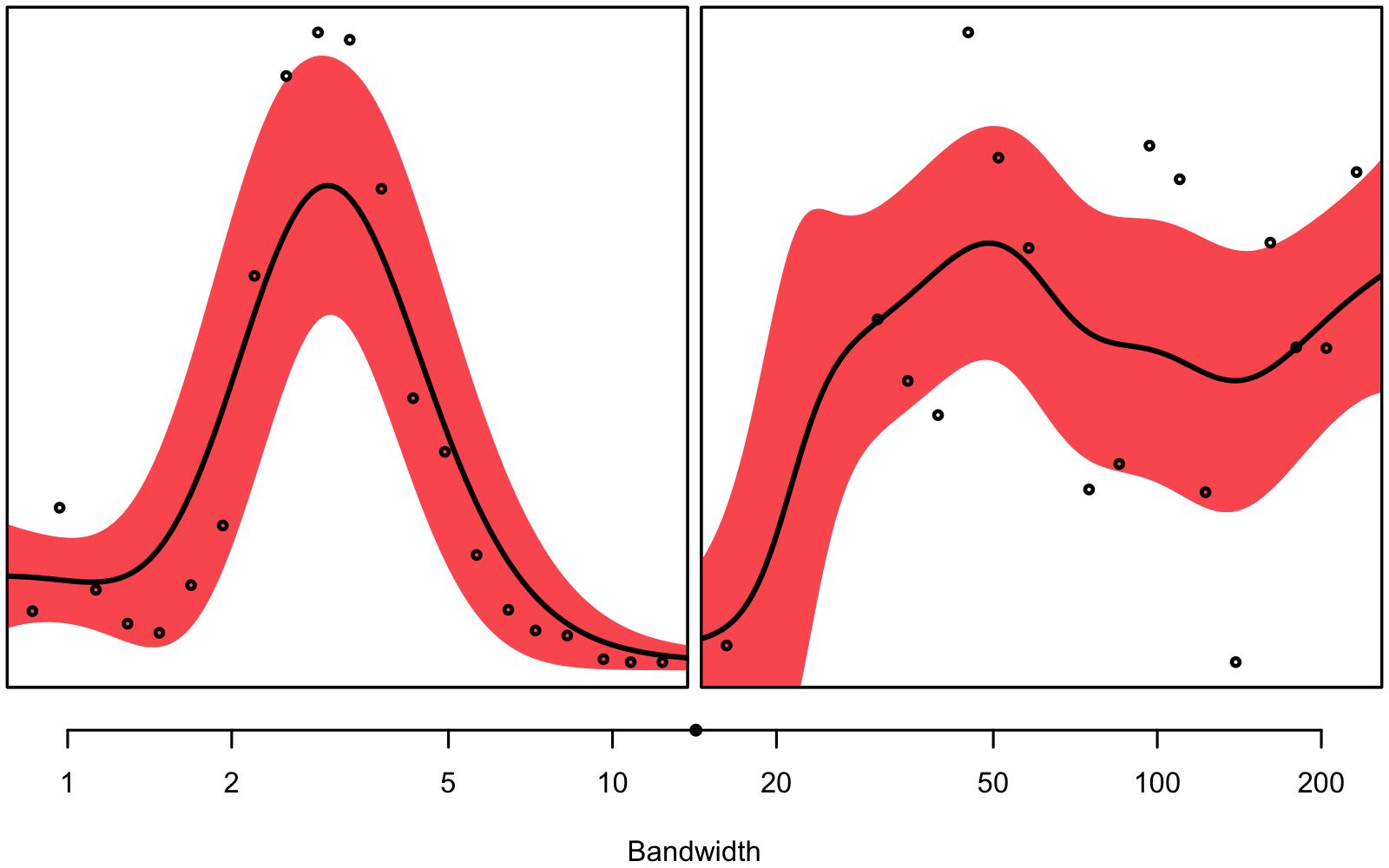
Figure 3.1: Animated explanation on two examplary subsets of the data. On the left, there is a very high signal to noise ratio, thus the optimal `bandwith` hyperparameter will be smaller than on the right.

The bandwidth hyperparameter is individually tuned using 3-fold 10 times repeated cross-validation for every combination of column and depth and variable¹, respectively. You can see an overview of the found hyperparameters in figure 3.2, 3.3, and 3.4.

¹ I.e. the three variables N₂O concentration, site preference and \(\delta\)¹⁸O.

Figure 3.2: Optimal hyperparameter size by depth and column for the N₂O-N concentration.

Figure 3.3: Optimal hyperparameter size by depth and column for the site preference.

Figure 3.4: Optimal hyperparameter size by depth and column for the stable isotope ratio \(\delta\)¹⁸O concentration.

Generally, smaller bandwidths correspond to a more flexible model, indicating a larger signal-to-noise ratio. Notice how deeper measurements seem to correspond to smaller bandwidths, at least for the N₂O concentration and the stable isotope ratio (\(\delta\)¹⁸O). Note that the optimal bandwidths for N₂O are also used for the interpolation of N₂O-N_volume and N₂O-N_area.

Numerical approximation of the derivative estimation

With the optimized hyperparameters, we are all set to estimate the functions over time, as well as their derivatives, which are needed for the process rate estimator.

One common way to numerically approximate the derivative of a function \(f\) at a point \(t\) is through the central difference method. This method computes the average rate of change over a small interval around the point of interest.

\[\frac{df}{dt} \approx \frac{f(t + h) - f(t - h)}{2h} \tag{3.4}\]

Here, \(h\) is a small positive number known as the step size. The notations \(f(t + h)\) and \(f(t - h)\) represent the function values at \(t + h\) and \(t - h\), respectively. The smaller h is, the more accurate the approximation should be. However, if h is too small, then round-off errors from computer arithmetic can become significant. So, an appropriate balance must be struck. The central difference method is implemented as the fderiv function in the pracma R package.

Both the function estimation as well as the estimation of the derivative are performed with a single function call in the R package PRE.

data <- getMissing(data = data, hyperparameters = PRE::hyperparameters)

Here, data is the data frame that we slightly extended with the getN2ON function. The object hyperparameters is a three-dimensional array containing the optimized hyperparameters for this project. It is also included in the PRE package².

² To optimize the hyperparameters, you can run the R script hypertuning.R.

3.4 Calculating the fluxes

Model parameters

Table 3.2: Overview of the parameters used in the model.

Symbol	Code	Name	Value	Unit
\(BD\)	`BD`	Bulk density (mass of the many particles of the material divided by the bulk volume)	\(1.686\)	g cm^-3
\(\theta_w\)	`theta_w`	Soil volumetric water content
\(\theta_a\)	`theta_a`	Air-filled porosity	\(1-\frac{\theta_w}{\theta_t}\)
\(\theta_t\)	`theta_t`	Total soil porosity	\(1-\frac{BD}{2.65}\)
\(\text T\)	`temperature`	Soil temperature	\(298\)	K
\(D_{\text{s}}\)	`D_s`	Gas diffusion coefficient	Equation 3.6	m²s^-1
\(D_{\text{fw}}\)	`D_fw`	Diffusivity of N₂O in water	Equation 3.8
\(D_{\text{fa}}\)	`D_fa`	Diffusivity of N₂O in air	Equation 3.9
\(D_{\text{fa,NTP}}\)		Free air diffusion coefficient under standard conditions	Equation 3.9
\(n\)	`n`	Empirical parameter (Massman 1998)	1.81
\(H\)	`H`	Dimensionless Henry’s solubility constant	Equation 3.7
\(\rho\)	`rho`	Gas density of N₂O	\(1.26 \times 10^6\)	mg m_-3

The diffusion fluxes between soil increments are described by Frick’s law (Equation 3.5).

\[F_{\text{calc}} = \frac{dC}{dZ} D_{\text s} \rho \tag{3.5}\]

Here, \(D_s\) is the gas diffusion coefficient, \(\rho\) is the gas density of N₂O, and \(\frac{dC}{dZ}\) is the N₂O concentration gradient from lower to upper depth. The fluxes are calculated based on N₂O concentration gradients between 105-135 cm, 75-105 cm, 45-75 cm, 15-45 cm, and 0-15 cm depth layers, and ambient air above the soil surface.

\(\theta_w\) is the soil volumetric water content, \(\theta_a\) the air-filled porosity, and \(\theta_T\) is the total soil porosity.

The gas diffusion coefficient \(D_{\text s}\) was calculated according Equation 3.6 as established by Millington and Quirk in 1961 (Millington and Quirk 1961).

\[D_{\text s} = \left( \frac{\theta_w^{\frac{10}{3}} + D_{\text fw}}{H} + \theta_a^{\frac{10}{3}} \times D_{\text fa} \right) \times \theta_T^{-2} \tag{3.6}\]

Here, \(H\) represents a dimensionless form of Henry’s solubility constant (\(H'\)) for N₂O in water at a given temperature. The constant \(H\) for N₂O is calculated as follows:

\[H = \frac{8.5470 \times 10^5 \times \exp \frac{-2284}{\text T}}{\text R \times \text T} \tag{3.7}\]

Here, \(\text R\) is the gas constant, and \(\text T\) is the temperature (\(\text T = 298 \; \text K\)).

\(D_{\text{fw}}\) was calculated according to Equation 3.8 as documented by Versteeg and Van Swaaij (1988) (Versteeg and Van Swaaij 1988).

\[D_{\text{fw}} = 5.07 \times 10^{-6} \times \exp \frac{-2371}{\text T} \tag{3.8}\]

\[D_{\text{fa}} = D_{\text{fa, NTP}} \times \left( \frac{\text T}{273.15} \right)^n \times \left( \frac{101'325}{\text P} \right) \tag{3.9}\]

Calculate mean moisture between depth increments:

\[ \theta_{w} = \frac{1}{2}(m_d + m_{d+1}) \tag{3.10}\]

Where \(m\) is the moisture and \(d\) is the depth index.

All the computations described in equations 3.5 3.6, 3.7, 3.9, 3.8 and 3.10 are performed by calling the following function from the R package PRE.

data <- calculateFluxes(data = data, parameters = getParameters())